| Definitions |  x:A. B(x), P x:A. B(x), P   Q, A & B, eventlist(pred?;e), P & Q, x f y, t Q, A & B, eventlist(pred?;e), P & Q, x f y, t  T, T,   x,y. t(x;y), Prop, x,y. t(x;y), Prop,   x. t(x), Y, if b x. t(x), Y, if b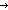 t else f fi, true t else f fi, true , false , false , P , P   Q, P Q, P   Q, P Q, P  Q, Q,  A, R^*, A, R^*,  x:A. B(x), x:A. B(x),  , rel_exp(T;R;n), A , rel_exp(T;R;n), A B, False, i= B, False, i= j, R^+, SQType(T), {T}, Unit, x(s1,s2), WellFnd{i}(A;x,y.R(x;y)), j, R^+, SQType(T), {T}, Unit, x(s1,s2), WellFnd{i}(A;x,y.R(x;y)),  , x(s), Dec(P), SWellFounded(R(x;y)), , x(s), Dec(P), SWellFounded(R(x;y)),  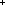 , ,  , S , S  T T |